La caractérisation statistique de la distribution de taille des événements peut parfois ne pas suffire pour déterminer l’aléa plausible en un lieu donné et sa période de retour. Ceci est vrai notamment si l’aléa est délocalisé, c’est-à-dire peut être véhiculé sur des distances très grandes.
Méthode
Ainsi, pour l’aléa sismique, il faut combiner plusieurs types de données : (i) les lois fréquence/magnitude au sein de chaque secteur du zonage sismotectonique qui donnent les probabilités d’occurrence annuelle de séismes de telle ou telle magnitude (ii) les lois liant magnitude, distance et accélération.
Cette combinaison permet alors de calculer en chaque point du territoire la probabilité annuelle d’être soumis à une accélération du mouvement du sol de telle ou telle valeur, et inversement de calculer la période de retour d’une accélération du mouvement du sol donnée.
Généralement, on préfère présenter une carte montrant l’accélération maximale correspondant à une période de retour fixée.
La carte ci-dessous montre une telle carte pour une période de retour de 475 ans.
Aléa sismique de la France.
Le Plan Séisme, un programme national de prévention du risque sismique.
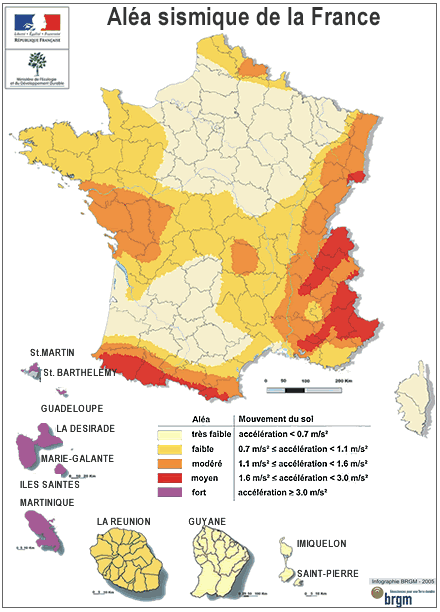
A des échelles plus réduites encore (de la ville voire du quartier), on définit un « microzonage » qui tient compte des divers effets de site pour pouvoir affiner le calcul de l’aléa et sa période de retour.
On peut procéder de même pour les autres aléas, en définissant par exemple la crue décennale, centennale, millénale, etc… dont les périodes de retour sont respectivement de dix, cent et mille ans.
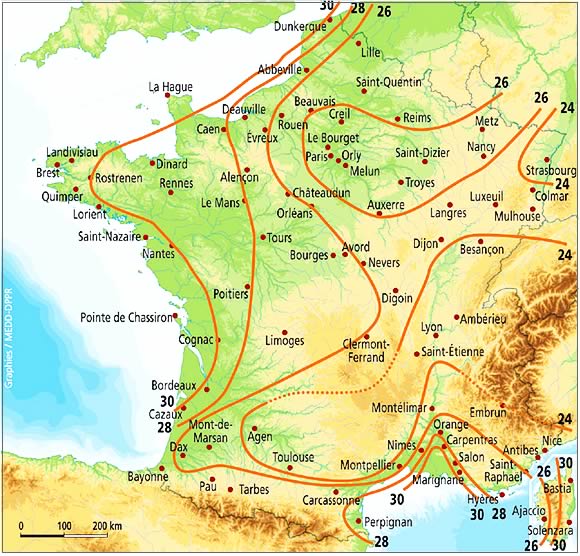
La figure ci-dessous montre la carte de vitesses des vents maximales (en m.s-1, à 10 mètres de hauteur en rase campagne) pour une période de retour de 50 ans en France métropolitaine.
Carte de vitesses maximales des vents pour une période de retour de 50 ans en France métropolitaine.
Méthode
Si un événement possède une période de retour T, cela signifie qu’à chaque instant t, la probabilité qu’il se produise dans l’intervalle [t ; t+dt] (où dt est petit) est :
P(t,dt,T) = dt/T
Cette probabilité est donc indépendante de t et le processus est dit poissonien stationnaire. Il est alors facile de montrer que la probabilité de ne pas observer le phénomène pendant une durée supérieure à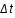 
est :
Prob(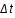 
,T) =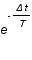 
Il en résulte que la probabilité d’observer au moins une fois le phénomène pendant un intervalle de durée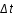 
est :
Pr(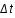 
,T) = 1 - Prob( 
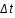,T) = 1 -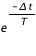 
Si l’on choisit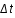 
=T, on voit donc que Pr(T,T) = 1 – 1/e = 0,63.
Cela signifie que si l’on considère une crue décennale, la probabilité d’observer au moins une crue de cette envergure en 10 ans est de 63%, et non 100% comme l’appellation « crue décennale » inciterait à le penser.
De même, il existe la même probabilité de 63% d’observer au moins une crue centennale en un siècle. On voit également que la probabilité de ne pas observer un événement pendant une durée égale à sa période de retour est de 1-0,63 =37%, qui est loin d’être négligeable.
La figure suivante montre l’évolution de Pr(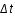
,T) (en bleu) et Prob(
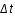,T) (en rouge) en fonction de 
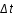/T.
Exemple
Cas de Parkfield (entre 1857 et 1966)
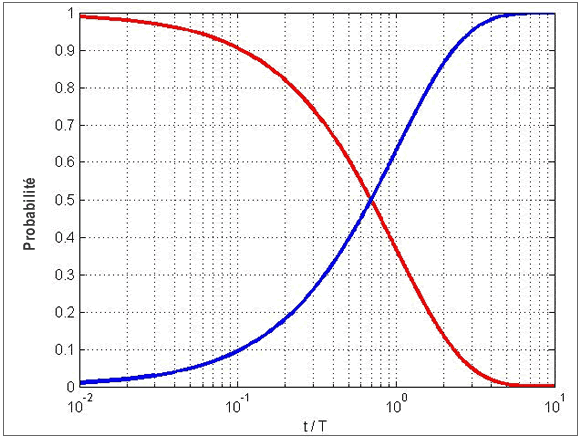
Si l’on reconsidère le cas de Parkfield, en ne tenant compte que des données observées entre 1857 et 1966, la période de retour T est estimée à 22 ans environ. Le dernier séisme s’y est produit en 2004, soit après une durée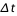 
de 38 ans.
Le rapport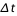 
/T étant de 1,7 la courbe rouge permet de réaliser qu’il y avait en fait environ 18% de chance d’observer un temps de récurrence au moins aussi grand. La courbe bleue montre qu’il y a le même nombre de chances d’observer un séisme dans un laps de temps inférieur à 4,4 ans.
Concernant la carte d’aléa sismique en France, on notera qu’une période de retour de 475 ans implique que l’aléa a 10% de chances d’être dépassé en 50 ans.
Remarque
L’approche par les processus poissoniens implique que la probabilité d’occurrence d’un événement ne dépend pas du temps, et en particulier pas du temps écoulé depuis l’événement précédent.
Si cela peut se justifier pour certains aléas, cette hypothèse va à l’encontre du concept de cycle sismique et de rebond élastique présenté plus haut dans le cas des séismes. En effet, on s’attend à ce que la probabilité d’occurrence d’un séisme sur une faille donnée soit faible si un séisme vient de s’y produire, et forte si le temps écoulé depuis le dernier en date est important. Ceci rejette donc l’hypothèse de processus poissonien.
Cependant, les tests statistiques montrent qu’aucun autre modèle probabiliste, même dépendant du temps, ne fait mieux qu’un modèle poissonien pour décrire les données observées.
Ceci traduit la longue route restant encore à parcourir pour marier concepts physiques et statistique dans le cas des séismes.
Page précédente
Page suivante