Tout corps dont la température est supérieure au zéro absolu (0° Kelvin équivaut à - 273°C) émet un rayonnement électromagnétique issu de l’agitation thermique des molécules, dont la longueur d’onde est fonction de la température.
Emission et absorption étant liées (loi du rayonnement de Kirchhoff), le physicien Max Planck en 1900 a imaginé ce qui se produirait dans le cas idéal du corps noir.
Définition
Loi de Planck :
Un corps noir est un corps hypothétique capable d’absorber puis de réémettre tout le rayonnement qui lui parvient, quelque soit la longueur d’onde. Il ne réfléchit, ni ne transmet aucun rayonnement. Planck a montré que l’énergie émise (luminance spectrale) par un corps noir dépendait uniquement de sa température.
avec :
c : vitesse de la lumière (3.108 m.s-1)
h : constante de Planck (6,625.10-34 J.s)
k : constante de Boltzmann (1,38.10-23 J.K-1)
T : température du corps noir en Kelvins
La loi de Planck décrit la répartition spectrale de l’énergie émise par un corps noir en fonction de sa température
Deux caractéristiques essentielles peuvent être dégagées de la figure ci-dessus :
Définition
L’énergie émise par un corps noir est d’autant plus importante que la température de ce dernier est élevée. Ce phénomène est décrit par la loi de Stefan - Boltzmann qui stipule que l’énergie émise par un corps noir augmente proportionnellement à la puissance quatrième de sa température :
M
T
=
σ
T
4
avec :
MT : l’exitance totale (énergie émise par unité de surface, en W.m-2) du corps noir
σ : la constante de Stefan - Boltzmann (5,67.10-8 J.K-4.m-2.s-1)
T : la température du corps en Kelvins
Définition
Selon la loi de Planck, à une température donnée, l’énergie émise par un corps noir passe par un maximum d’émission. La loi de Wien décrit la relation entre la longueur d’onde du maximum d’émission (λ
max) et la température du corps noir. Elle stipule que la longueur d’onde du maximum d’émission est inversement proportionnelle à sa température. Plus la température du corps noir augmente, plus le maximum d’exitance se déplace vers les courtes longueurs d’onde.
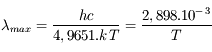
avec :
λ
max : longueur d’onde du maximum d’émission, exprimée en mètre
c : vitesse de la lumière (3.108 m.s-1)
h : constante de Planck (6,625.10-34 J.s)
k : constante de Boltzmann (1,38.10-23 J.K-1)
T : température du corps noir en Kelvins
Le soleil peut être assimilé à un corps noir dont la température de surface est de l’ordre de 5780°K. En appliquant la loi de Wien, on constate que le maximum d’émission du soleil correspond à une longueur d’onde de 0,5μm ce qui correspond au visible et au maximum de sensibilité de nos yeux. Le soleil étant la source la plus importante de rayonnements électromagnétiques sur Terre, certains évolutionnistes voient dans cette coïncidence une adaptation de la sensibilité de notre œil au domaine spectral qui reçoit le maximum de rayonnement solaire.
Le même exercice appliqué à la surface terrestre dont la température moyenne est d’environ 15°C (288°K), donne un maximum d’émission pour notre environnement aux alentours de 10μm. Ce rayonnement situé dans l’infrarouge thermique donne une bonne indication des températures de surface des objets.
Mais la Terre et de manière générale la plupart des surfaces naturelles ne sont pas des corps noirs. Ils n’absorbent pas totalement le rayonnement qu’ils reçoivent, mais en réfléchissent ou en transmettent une partie. On parle alors de « corps gris ». Pour une même température, un corps gris n'émet jamais autant qu'un corps noir. Le rapport entre les exitances (ou les luminances spectrales) du corps gris et du corps noir définit l'émissivité spectrale. Le coefficient d'émissivité d'une surface naturelle, noté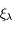 
a toujours une valeur inférieure à 1.
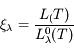
avec :
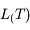: luminance spectrale de la surface naturelle à la température T
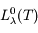: luminance spectrale du corps noir à la même température T
Luminances spectrales comparées d'un corps noir et d'un corps gris à une température T donnée
Page précédente
Page suivante